Formal Metrics

A review of formal metrics for quantifying "division" or "polarization".

Our aim with this work is to improve our capacity to develop systems that satisfy the bridging goal: an increase mutual understanding and trust across divides, creating space for productive conflict, deliberation, or cooperation. Here we list metrics that have been used in related literature.

Context

The metrics are designed to summarize an abstract model of the public sphere, which we assume is either a graph (e.g. figure A, or a network of Twitter followers) or a set of points in Euclidean space (e.g. figure B, or user embeddings on a social media platform).

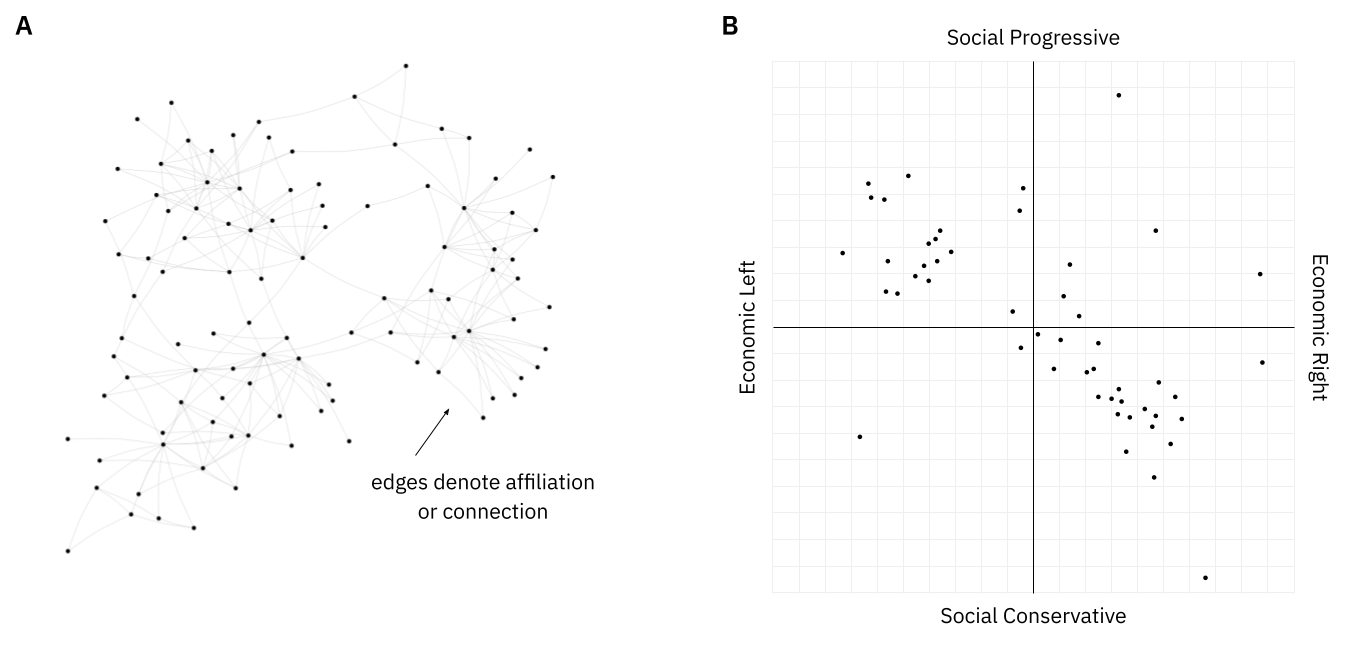
Simple examples of graph-based and space-based relation models.

As per the terminology introduced in the paper, these are examples of relation metrics, because they summarize the state of a relation model at a give point in time. In contrast bridging metrics—not yet reviewed here—summarize a change in relation metrics over time.

Caution

While the metrics below are presented as possible measures of this “bridging goal”, most are obviously not plausible measures. The best we can say about them is that we do not yet know whether they are good measures. For this reason, none of the metrics on this page should be used as optimization targets in an attention-allocator (such as a social media platform) without considerable care to monitor and avoid unintended consequences.

Also, note that these metrics are simply summaries of the structure of some abstract model, such as a graph-based or space-based relation model. The provenance or “semantics” of the underlying relation model is also important to consider. For example, a given metric may be an excellent measure of the bridging goal when applied to a relation model that captures goodwill between people, but be a poor measure when applied to a relation model that captures similarities in people’s patterns of engagement on social media. At present, we know very little about which types of relation models and which relation metrics can be validly used as a basis for bridging.

Table of Metrics

To toggle fullscreen mode, use your Esc key or the purple button in the table.

Metric	Intuition	Scope group individual population	Model Type graph groups space	Structure Required bounded space groups groups (exactly 2) signed edges NONE	Safe to Optimize? Maybe No	Formula	References
node-level homophily	The proportion of a vertex's neighbours which are in its own group.	individual	graph	groups	No	$\frac{d_{i} (v)}{d (v)}$	Currarini et al. (2009), Interian + Ribeiro (2018), Reese et al. (2007), Interian et al. (2022)
group-level homophily	An average measure of the degree to which vertices in a group are connected to vertices in their own group, rather than others.	sub-group	graph	groups	No	$\frac{\sum_{v \in G_{i}} d_{i} (v)}{\sum_{v \in G_{i}} d (v)}$	Lelkes (2016), Currarini et al. (2009), Interian et al. (2022)
population homophily	An average measure of the degree to which all vertices are connected to vertices in their own group, rather than others.	population	graph	groups	No	$\frac{\sum_{v \in V} d_{s (v)} (v)}{\sum_{v \in V} d (v)}$	Interian et al. (2022)
modularity	The number of intra-group edges in the graph minus the expected number of intra-group edges in a graph with the same nodes, groups and degrees, but with edges placed at random. (Up to a multiplicative constant.)	population	graph	groups	No	$\frac{1}{4 \| E \|} \sum_{u, v \in V, v \neq u} [1 ((u, v) \in E) - \frac{d (u) d (v)}{2 \| E \|}] 1 (u, v in same group)$	Newman (2006), Zhang et al. (2007), Wolfowicz et al. (2021), Garcia et al. (2015), Dal Maso et al. (2014), Interian et al. (2022)
E-I index	The difference between the proportions of edges that are inter- and intra-group.	population	graph	groups	No	$\frac{\| {(u, v) \in E : g (u) \neq g (v)} \| - \| {(u, v) \in E : g (u) = g (v)} \|}{\| E \|}$	Krackhardt + Stern (1988), Interian et al. (2022)
random walk controversy	Given that two random walks ended in different groups, the difference between the probability that they started from those same groups and the probability that they started from different groups.	population	graph	groups (exactly 2)	Maybe	$\begin{array}{rc} P (R_{1} (start) \in G_{1}, R_{2} (start) \in G_{2} ∣ R_{1} (end) \in G_{1}, R_{2} (end) \in G_{2}) \\ - P (R_{1} (start) \in G_{2}, R_{2} (start) \in G_{1} ∣ R_{1} (end) \in G_{1}, R_{2} (end) \in G_{2}) \end{array}$	Garimella et al. (2018), Garimella et al. (2016), Cossard et al. (2020), Rumshisky et al. (2017), Emamgholizadeh et al. (2020), Interian et al. (2022)
node-level random walk controversy	The probability that a random walk which ends in one group started at the vertex of interest, relative to the same value for other groups.	individual	graph	groups	No	$\frac{P (R (start) = v ∣ R (end) \in G_{i}^{+})}{\sum_{j = 1}^{M} P (R (start) = v ∣ R (end) \in G_{j}^{+})}$	Garimella et al. (2018), Garimella et al. (2016), Cossard et al. (2020), Rumshisky et al. (2017), Emamgholizadeh et al. (2020), Interian et al. (2022)
degree of balance	Degree of consistency with properties such as "my friend's friend is my friend" and "my friend's enemy is my enemy".	population	graph	signed edges	Maybe	$\frac{c_{+} (G)}{c (G)}$	Harary (1959), Aref et al. (2020), Interian et al. (2022)
line index of balance	Minimum number of edge modifications that must be made to be perfectly consistent with properties such as "my friend's friend is my friend" and "my friend's enemy is my enemy".	population	graph	signed edges	Maybe	Not easily notated—see references.	Harary (1959), Aref et al. (2020), Interian et al. (2022)
point index of balance	Minimum number of vertices which must be deleted to be perfectly consistent with properties such as "my friend's friend is my friend" and "my friend's enemy is my enemy".	population	graph	signed edges	Maybe	Not easily notated—see references.	Harary (1959), Aref et al. (2020), Interian et al. (2022)
diameter	The maximum distance between any two points.	population	space		No	$max_{x, y \in X} ‖ x - y ‖$	Bramson et al. (2016), Bramson et al. (2017)
volume	The volume of the minimal convex polytope that includes all points.	population	space		No	$min {Volume (S) ∣ X \subseteq S, S convex}$	Bramson et al. (2016), Bramson et al. (2017)
mean difference	Average pairwise distance between any two points.	population	space		No	$\frac{1}{(\binom{N}{2})} \sum_{x, y \in X, x \neq y} ‖ x - y ‖$	Bramson et al. (2016), Bramson et al. (2017)
average absolute deviation	Average distance between each point and the mean.	population	space		No	$\frac{1}{N} \sum_{x \in X} ‖ x - \bar{x} ‖$	Bramson et al. (2016), Bramson et al. (2017)
standard deviation	Scalar standard deviation of the set of points.	population	space		No	$\sqrt{\frac{1}{N} \sum_{x \in X} ‖ x - \bar{x} ‖^{2}}$	Bramson et al. (2016), Bramson et al. (2017)
variance	Scalar variance of the set of points.	population	space		No	$\frac{1}{N} \sum_{x \in X} ‖ x - \bar{x} ‖^{2}$	Bramson et al. (2016), Bramson et al. (2017)
coefficient of variation	Scalar standard deviation divided by the mean.	population	space		No	$\frac{1}{\bar{x}} \sqrt{\frac{1}{N} \sum_{x \in X} ‖ x - \bar{x} ‖^{2}}$	Bramson et al. (2016), Bramson et al. (2017)
coverage	The number of distinct attitudes held or the variety of attitudes that at least one person in the population holds.	population	space	bounded space	No	$Volume (⋃_{x \in X} B_{r} (x)) / Volume (X)$	Bramson et al. (2016), Bramson et al. (2017)
fragmentation	The number of groups.	population	space	groups	No	$M$	Bramson et al. (2016), Bramson et al. (2017)
mean group significance	Average pairwise $p$ -value in pairwise hypothesis tests for the difference between two groups.	population	space	groups	No	$\frac{1}{(\binom{M}{2})} \sum_{i < j} pValue (H_{1} : G_{i} \neq G_{j} against H_{0} : G_{i} = G_{j})$	Bramson et al. (2016), Bramson et al. (2017)
mean group distance	Average pairwise distance (using a probability metric) between the distributions of groups.	population	space	groups	No	$\frac{1}{(\binom{M}{2})} \sum_{i < j} ProbabilityMetric (G_{i}, G_{j})$	Bramson et al. (2016), Bramson et al. (2017)
(multi)modality	The extent to which a distribution is bimodal or multimodal.	population	space		No	There are a number of existing measures—see references.	Knapp (2007), Nason + Sibson (1992), Bramson et al. (2016), Bramson et al. (2017)
divergence of means	Average pairwise distance between group means.	population	space	groups	No	$\frac{1}{(\binom{M}{2})} \sum_{i < j} ‖ Mean (G_{i}) - Mean (G_{j}) ‖$	Bramson et al. (2016), Bramson et al. (2017)
deviation from means	Average distance between an individual and the mean of their group, averaged across groups.	population	space	groups	No	$\frac{1}{M} \sum_{i = 1}^{M} \frac{1}{n_{i}} \sum_{x \in G_{i}} ‖ x - Mean (G_{i}) ‖$	Bramson et al. (2016), Bramson et al. (2017)
size parity	A measure of polarization based only on the proportions of points in each group.	population	groups	groups	Maybe	$- \frac{1}{\log M} \sum_{i = 1}^{M} (\frac{n_{i}}{N}) \log (\frac{n_{i}}{N})$	Bramson et al. (2016), Bramson et al. (2017)

Notation

Here, we introduce the notation used in the formulae in the above table. The notation differs by model type.

Graph

Let $G = (V, E)$ denote a (mathematical) graph, where $V$ is the set of vertices and $E$ is the set of edges. Optionally, the vertices may each belong to one of $M$ groups, denoted $G_{1}, \dots, G_{M}$ , which form a partition of $V$ . For a vertex $v \in V$ , we use $d (v)$ to denote the degree of the vertex and $d_{i} (v)$ to denote the numbe of vertices in group $i$ to which $v$ is connected. If there are groups, $g (v)$ refers to the group which contains vertex $v$ .

There are a few more specific notations that are only used in a small number of metrics.

$R (t)$ denotes a random walk on the graph, as a function of time $t$ . In the formulae, we simply write $R (start)$ or $R (end)$ , which should be interpreted in the intuitive way.
For a given $1 < i < M$ , $G_{i}^{+}$ denotes the set of $k$ highest-degree nodes in group $G_{i}$ .
If $G$ is a signed graph, $G = (V, E^{+}, E^{-})$ , then $c (G)$ denotes is the number of 3-cycles in a graph, and $c_{+} (G)$ is the number of positive 3-cycles in a graph, where the sign of a cycle is the product of the signs of its edges.

Space

Let $X$ be a set of $N$ points in some metric space $R$ . Optionally, the points may each belong to one of $M$ groups, denoted $G_{1}, \dots, G_{M}$ , which form a partition of $X$ . The number of points in group $G_{i}$ is denoted $n_{i}$ . We use $\bar{x}$ to denote the mean of the points in $X$ , and $B_{r} (x)$ to denote a ball of radius $r$ centered on a given point $x \in X$ .